[Vietnamese] Dynamic Programming - Longest common subsequence

Trong quá trình chia nhỏ bài toán lớn thành các bài toán con để giải và kết hợp lại để được lời giải bài toán lớn, chúng ta sẽ thấy nhiều kết quả bài toán con có thể bị tính trùng lặp. Để tránh việc này, phương pháp Quy hoạch động sử dụng một bảng để lưu các kết quả của bài toán con và khi cần thì ta chỉ việc gọi ra sử dụng. Do đó phương pháp này thường tỏ ra khá hiệu quả trong các bài toán tin (đặc biệt 2 dạng bài tìm nghiệm tối ưu, đếm cách) và các câu hỏi coding interview.

Chúng ta sẽ cùng tìm hiểu phương pháp này thông qua cách tiếp cận các bài toán kinh điển.

1. Longest common subsequence

1.1. Xác định B có phải là xâu con của A hay không?

Problem 1. Cho 2 xâu ký tự (chỉ bao gồm các chữ cái Latin) A và B. Định nghĩ B là xâu con của A nếu như từ xâu A ta xóa đi một số ký tự thì thu được xâu B. Hãy xác định xem B có phải là xâu con của A hay không?

Trước tiên thử lấy một ví dụ minh họa:

Mình có xâu A = aabb và xâu B = ba. Theo định nghĩa của đề bài thì B không phải là xâu con của A. Nhưng làm thế nào để code được?

Mình sẽ duyệt bắt đầu từ cả 2 xâu để xác định nếu phần tử thứ i của xâu A trùng với phần tử đầu tiên của xâu B thì tăng biến duyệt ở cả 2 xâu lên, còn không thì mình tăng biến duyệt ở xâu A và giữ nguyên ở xâu B. Nếu A kết thúc mà biến duyệt ở B chưa kết thúc thì B không phải là xâu con của A, ngược lại thì B là xâu con của A. Sử dụng hai con trỏ (two pointers) sẽ giúp tăng tốc độ duyệt của thuật toán!

function isSubsequence(a, b) {
  if (a.length === 0 || b.length === 0) return false

  let first = 0, second = 0;
  while (first < a.length && second < b.length) {
    if (a[first] === b[second]) {
      first++;
      second++;
    } else {
      first++;
    }
  }
  if (second < b.length) return false;
  return true;
}

Do mình phải duyệt cả hai xâu nhưng duyệt này không phải dạng lồng nhau mà là duyệt song song nên độ phức tạp của thuật toán trên là O(n + m) với n, m tương ứng là độ dài 2 xâu A, B.

1.2. Tìm xâu con C của cả A và B sao cho C dài nhất (LCS - Longest common sequence)

Problem 2. Tìm độ dài xâu con chung dài nhất của A và B

Để giải bài này, mình có thể suy nghĩ cách áp dụng bài trước là từ xâu B (hoăc A) sinh ra tất cả các xâu con của nó. Sau đó xem xét xâu con đó có phải là xâu con của A không (bài 1.1), nếu phải thì mình xét tiếp nó có dài nhất hay không.

Như vậy với một xâu B có n phần tử, thì số xâu con sinh ra là bao nhiêu? Câu trả lời là \(2^n\). Như vậy, theo thuật toán này, độ phức tạp của chúng ta sẽ là \(2^n(n + m)\)! Một con số quá lớn.

Do phương án duyệt trâu (brute force) không dùng được trong trường hợp này, nên mình cần một công cụ khác hiệu quả hơn. Bây giờ viết thử A, B, C ra xem và hy vọng sẽ thu được nhận xét gì đó:

A=a1a2...an B=b1b2...bm C=c1c2..ck,(k<m,n)

Nếu \(a_n\) và \(b_m\) trùng nhau, thì \(c_k = a_n = b_m\) (để đảm bảo tính dài nhất). Khi đó ta gọi C′=c1c2...cl,(l=k−1) là xâu con chung của \(A' = a_1a_2...a_p, (p = n - 1)\) và \(B' = b_1b_2...b_q, (q = m - 1)\) hoặc có thể viết lại thành \(C = LCS(A', B') + 1\)
Nếu \(a_n\) khác \(b_m\) khi đó \(c_k\) có thể nhận 3 trường hợp:
- Nếu \(c_k = a_n\): khi đó thì \(C = LCS(A', B)\)
- Nếu \(c_k = b_m\): khi đó thì \(C = LCS(A, B')\)
- Nếu \(c_k\) khác \(a_n, b_m\): khi đó thì \(C = LCS(A', B')\)

Như vậy trong trường hợp này ta cần tìm là C=Max(LCS(A′,B),LCS(A,B′),LCS(A′,B′))

Tuy nhiên do \(LCS(A', B')\) luôn nhỏ hơn \(LCS(A, B')\) và \(LCS(A', B)\) nên mình có thể viết lại: C=Max(LCS(A′,B),LCS(A,B′))

function solveLCS (a, b) {
  function LCS(n, m) {
    if (n * m === 0) return 0;

    if (a[n-1] === b[m-1]) return LCS(n-1, m-1) + 1;
    return Math.max(LCS(n-1, m), LCS(n, m-1));
  }

  return LCS(a.length, b.length);
}

Tương tự như bài toán tính số Fibonacci thứ n, lời giải đệ quy ở trên sẽ đi tính lại (trùng lặp) các \(LCS\) con (được tô vàng trong cây đệ quy minh họa bên dưới).

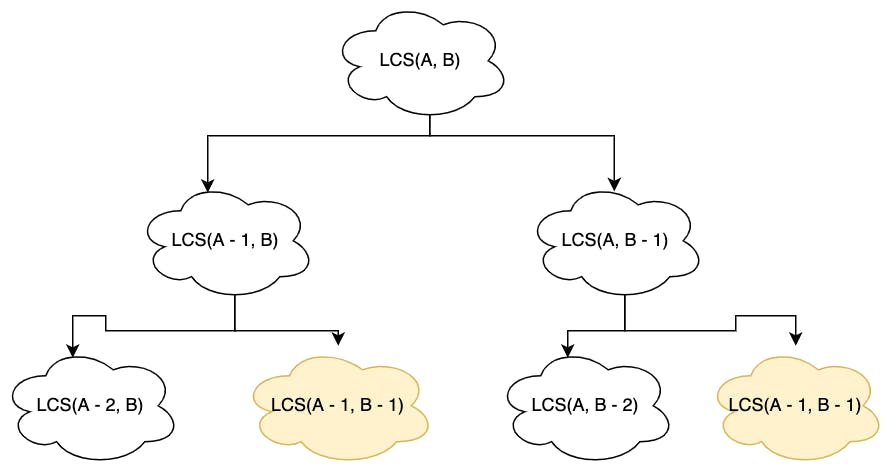
Để tránh phải tính lại các giá trị này, trong bài Fibonacci, kỹ thuật dùng một mảng để lưu lại các giá trị này sau đó nếu cần ta sẽ lôi chúng ra dùng được gọi là đệ quy có nhớ hay quy hoạch động. Tuy nhiên có một khác biệt so với bài Fibonacci là mảng nhớ mình dùng là mảng 1 chiều, còn bài này do có 2 xâu cần xử lý nên mình sẽ sử dụng mảng 2 chiều. Do mảng hai chiều thường ít sử dụng trong các công việc hằng ngày hơn mảng 1 chiều và JavaScript không hỗ trợ mặc định multidimensional array nên mình sẽ nói về nó một chút trước khi chúng ta quay lại bài toán này.

1.3. Mảng hai chiều

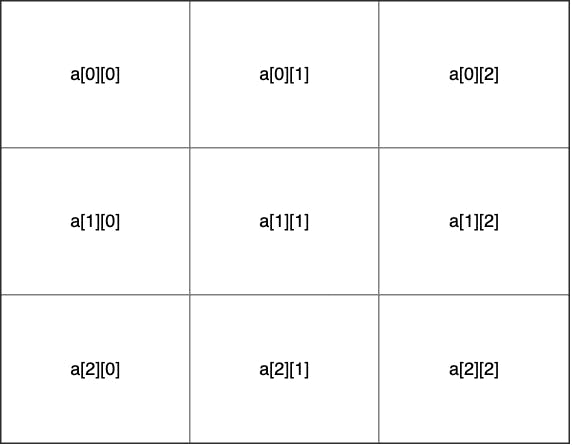
Trong hình minh họa mảng hai chiều ở trên, chúng ta thấy rằng mỗi phần tử trong mảng hai chiều được index bằng 2 chỉ số hàng và cột. Do trong ngôn ngữ JS không hỗ trợ, nên trường hợp này mình có thể làm bằng cách tạo ra mảng 1 chiều gồm n phần tử tương ứng với \(n\) hàng và ứng với mỗi hàng, mình gán giá trị là một mảng gồm m phần tử tương ứng với \(m\) cột.

Với cách làm này mình cũng có thể truy xuất đến phần tử hàng \(i\) cột \(j\) trong mảng bằng truy vấn \(a[i][j]\). Chúng ta có thể khởi tạo một mảng hai chiều trong JS với kích thước \(n * m\) như sau:

const array = new Array(n).fill(0).map(x => new Array(m).fill(0));

Đối với mảng hai chiều, khi cần thực hiện vòng lặp qua tất cả các phần tử của mảng, chúng ta cần 2 vòng for lồng nhau

for (let i = 0; i < n; i++) {
  for (let j = 0; j < m; j++) {
    // do something with a[i][j]
    console.log(a[i][j]);
  }
}

1.4. Giải bài toán LCS bằng quy hoạch động

Sau khi biết được mảng hai chiều dùng để lưu kết quả các bài toán con, chúng ta sẽ khởi tạo một mảng hai chiều ban đầu tất cả các phần tử nhận giá trị 0. Một lưu ý nhỏ nữa là mảng hai chiều này của mình sẽ duyệt lấy giá trị từ 1 đến length thay vì 0 đến length - 1 vì mình phải chừa ra 2 đầu mút? (Mọi người thử suy nghĩ xem tại sao :) )

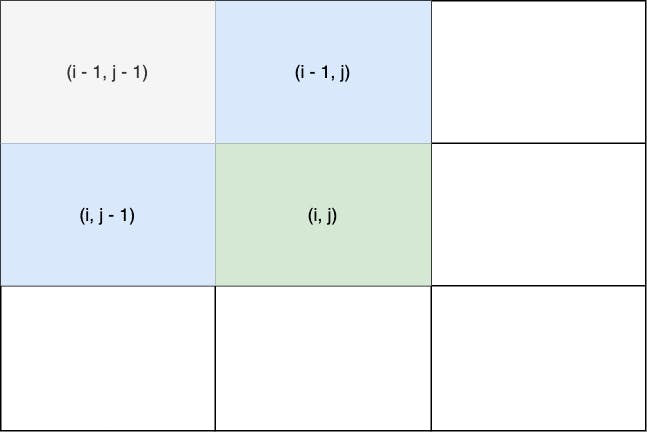
Sau đó, chúng ta duyệt qua lần lượt các phần tử trong mảng. Giả sử đến vị trí \((i, j)\) (hàng \(i\) và cột \(j\)) được tô xanh lá như hình dưới, khi đó theo công thức ở 1.3 thì \(LCS(i, j)\) sẽ nhận giá trị giống ô \((i - 1, j - 1)\) nếu \(a[i-1] = b[j-1]\), ngược lại thì sẽ lấy giá trị lớn nhất trong hai ô tô xanh dương.

Có thể thấy tại một vị trí \((i, j)\) bất kỳ thì mình sẽ chỉ cần lấy ra 3 ô tương ứng 3 vị trí mà đã được tính toán trước đó để xét, các giá trị này đã được lưu lại trong mảng nên mỗi lần gọi truy vấn mình không cần phải tính toán lại như trường hợp 1.3

function dpLCS(a = '', b = '') {
  let lcs = new Array(a.length + 1).fill(0).map(x => new Array(b.length + 1).fill(0));

  for (let i = 1; i <= a.length; i++) {
    for (let j = 1; j <= b.length; j++) {
      if (a[i - 1] === b[j - 1]) {
        lcs[i][j] = lcs[i - 1][j - 1] + 1;
      }
      else {
        lcs[i][j] = Math.max(lcs[i][j - 1], lcs[i - 1][j]);
      }
    }
  }

  return lcs[a.length][b.length];
}

Trong lời giải này, có thể thấy ngay độ phức tạp của thuật toán là \(O(m * n)\) còn trong lời giải 1.3 bằng đệ quy thì việc xác định độ phức tạp của thuật toán khó khăn hơn (hẹn mọi người một bài viết về chủ đề này trong tương lai).

2. Longest Palindrome subsequence (LPS)

Problem 3. Cho một xâu ký tự A (chỉ gồm các chữ cái Latin). Quy ước rằng khi xóa đi một số ký tự trong xâu A thì ta thu được xâu mới gọi là xâu con của A. Hãy tìm xâu con đối xứng (palindrome) dài nhất trong A.

Ở bài toán này, tương tự bài trước, mình cũng có một kỹ thuật duyệt trâu (brute force) là liệt kê tất cả các xâu con của A. Sau đó viết hàm kiểm tra xem xâu con đó có đối xứng hay không, nếu có thì mình xét tiếp đến độ dài để lấy ra độ dài dài nhất.

Hàm kiểm tra xâu có phải đối xứng hay không mình có thể dùng kỹ thuật hai con trỏ (two pointers). Một con trỏ ở đầu và một con trỏ ở cuối, dịch chuyển hai con trỏ lại gần nhau, nếu tồn tại một vị trí mà \(str[i] \neq str[j]\) thì return false, ngược lại khi đến \(\left \lfloor \frac{length}{2} \right \rfloor\) thì return true. Tuy nhiên, trong JS có thể code gọn đẹp hơn như sau:

function isPalindrome(str) {
    return str === str.split("").reverse().join("");
}

Giả sử xâu A có dạng \( A = a_1a_2...a_n\). Do một xâu đối xứng thì sẽ có hai phần tử đầu và cuối giống nhau nên mình xét trường hợp nếu \(a_1 = a_n\), lập luận tương tự như bài LCS, mình có công thức \(L(0, n-1) = L(2, n-2) + 2\). Trường hợp \(a_1\) khác \(a_n\) thì \(L(0, n-1) = \textrm{Max}(L(1, n-2), L(2, n-1))\)

Bài này mình cũng code thử bằng đệ quy (recursive) trước xem như thế nào, rồi sẽ chuyển sang lời giải bằng quy hoạch động. Cách làm này các bạn có thể áp dụng trong lúc phỏng vấn vì nhiều bài việc tạo bảng quy hoạch động không hề dễ ngay từ lúc đầu!


function solveLPS(seq, i, j) {

  // case: only one character
  if (i === j) return 1;

  // case: only two same characters
  if (seq[i] === seq[j] && i + 1 === j) {
    return 2;
  }

  // case: first and last characters match
  if (seq[i] === seq[j]) {
    return solveLPS(seq, i + 1, j - 1) + 2;
  }

  return Math.max(solveLPS(seq, i, j - 1), solveLPS(seq, i + 1, j));
}

/**
 * 
 *              L(0, 5)
             /        \ 
            /          \  
        L(1,5)          L(0,4)
       /    \            /    \
      /      \          /      \
  L(2,5)    L(1,4)  L(1,4)  L(0,3)

 */

Đoạn code trên là lời giải đệ quy cho bài LPS cùng với minh họa cây đệ quy cho trường hợp n = 6 và các ký tự trong chuỗi đôi một khác nhau. Tương tự như cây đệ quy của bài LPS, nếu mình vẽ hết thì có rất nhiều bài toán con được tính trùng lặp. Đến đây, mình sẽ suy nghĩ sử dụng mảng để lưu lại các kết quả trước đó, có 2 chỉ số mình quan tâm là \(i, j\) nên khả năng bảng của mình phải là một mảng hai chiều.

Chris Dinh - Software Engineer @ NAB