Một số kỹ thuật xử lý trên mảng
Bài này sẽ là một số ghi chép của mình về các kỹ thuật để xử lý khi đứng trước một bài toán lập trình. Toàn bộ các kỹ thuật này mình minh họa trên cấu trúc dữ liệu mảng và cài đặt bằng ngôn ngữ JavaScript.
Có thể các kỹ thuật này, với một số chỉnh sửa, sẽ có thể được áp dụng trong các cấu trúc dữ liệu phức tạp hơn. Tuy nhiên, mình thấy mảng là một cấu trúc dữ liệu khá phổ biến và dễ minh họa nhất.
Một số lưu ý:
- Mảng là một vùng nhớ có kích thước cố định (fixed-size), liên tục (contiguous)
- Các thao tác ghi một phần tử và lấy một phần tử ra khỏi mảng (store and access) mất time complexity là \( O(1) \).
Do tính tiện dụng của mảng, có nhiều data structures khác sử dụng mảng cho việc implementation ví dụ như strings, stacks, queues và hash tables.
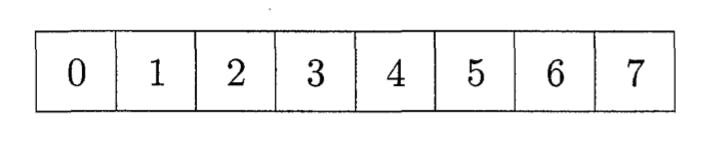
Mỗi phần tử của mảng đều được gắn một chỉ số (index) để giúp cho việc tìm kiếm (lookup) phần tử tại vị trí \( i \), truy vấn \(a[i] \) diễn ra nhanh chóng. Trong hình minh họa trên, mảng đã cho có chiều dài bằng \( 8 \) với các phần tử \( a[0] = 0, a[1] = 1, ..., a[7] = 7 \).
Mảng cũng có một số hạn chế. Ví dụ như việc tìm kiếm một phần tử mang giá trị cụ thể nào đó (không giống việc tìm phần tử có index như trên) đòi hỏi mình phải duyệt toàn bộ mảng. Xóa (delete) một phần tử trong mảng nghĩa là mình sẽ dịch chuyển các phần tử đứng sau nó sang bên trái 1 đơn vị, tốn \(O(n)\) time operation. Tương tự, thêm (insert) một phần tử mới vào mảng yêu cầu mình phải dịch chuyển các phần tử đăng sau nó sang phải 1 đơn vị, cũng tốn \( O(n) \) time operation.
Một hạn chế khác cũng thường xuyên được nhắc đến là mảng là một kiểu cấu trúc fixed bound nên mảng sẽ không phù hợp để lưu trữ tập hợp các elements mà mình không biết size (kích thước) ban đầu.
Một số bài toán minh họa
1. Get products of all other elements
Viết một hàm nhận vào một mảng gồm các số nguyên và trả về một mảng mới sao cho phần tử thứ \( i \) trong mảng mới bằng tích các phần tử trong mảng cũ nhưng không tính phần tử \(i \).
Example: hàm \(f\) nhận vào mảng \( [1, 2, 3, 4, 5] \) và sẽ trả ra kết quả \([120, 60, 40, 30, 24]\).
Follow-up: liệu mình có thể giải bài này mà không dùng phép chia?
Lời giải bài toán này dùng phép chia rất đơn giản, đầu tiên mình lặp qua mảng input một lần để tính tích tất cả các phần tử trong mảng. Sau đó ở lần lặp thứ 2, tại phần tử thứ \(i\) mình có \(newArr[i] = \dfrac{product}{input[i]}\)
function products(input) {
if (input.length === 0) return [];
let prod = 1;
for (let i = 0; i < input.length; i++) {
prod *= input[i];
}
let results = new Array(input.length).fill(null);
for (let i = 0; i < input.length; i++) {
results[i] = prod / input[i];
}
return results;
}
Để giải bài toán follow-up, không dùng phép chia, có một kỹ thuật thường được áp dụng cho các mảng là: thực hiện tính toán trên các mảng con, và sau đó build up solution dựa trên các mảng con đó.
Technique 1: precomputing results from subarrays, and building up a solution from these results
Đề bài yêu cầu mình tính tích của các phần tử trong mảng \(input\) ngoại trừ phần tử \(i\) nên mình có thể nghĩ đến hình ảnh phần tử \(i\) chia mảng \( input\) thành 2 phần trước và sau, gọi là \( suffix \) array và \( prefix \) array. Đây chính là 2 subarrays mà kỹ thuật này muốn nói đến.
Cụ thể, để tính \( prefix\) array mình sẽ lấy tích của các phần tử đứng trước \(i\) nhân với phần tử \(i\) và tương tự với mảng \(suffix\) mình sẽ lấy tích của các phần tử đứng sau \(i\) nhân với phần tử \(i\). Một tips nhỏ ở đây là mảng \( suffix \) sẽ được xây dựng bằng cách lặp duyệt ngược từ sau ra trước các phần tử trong mảng \( input \), sau đó mình đảo lại mảng \( suffix \) để có được thứ tự đúng.
function productsFollowingUp(input) {
if (input.length === 0) return [];
// Precomputing prefix sum
let prefix = new Array(input.length).fill(null);
for (let i = 0; i < input.length; i++) {
if (prefix[i - 1]) {
prefix[i] = prefix[i - 1] * input[i];
} else {
prefix[i] = input[i];
}
}
// Precomputing suffix sum
let suffix = new Array(input.length).fill(null);
let reverseInput = input.reverse();
for (let i = 0; i < reverseInput.length; i++) {
if (suffix[i - 1]) {
suffix[i] = suffix[i - 1] * reverseInput[i];
} else {
suffix[i] = reverseInput[i];
}
}
suffix.reverse();
// Compute the results based on subarray results
let results = new Array(input.length).fill(null);
for (let i = 0; i < results.length; i++) {
if (i === 0) {
results[i] = suffix[i + 1];
} else if (i === results.length - 1) {
results[i] = prefix[i - 1];
} else {
results[i] = prefix[i - 1] * suffix[i + 1];
}
}
return results;
}
console.log(productsFollowingUp([1, 2, 3, 4, 5]));
Độ phức tạp về time và space complexity cho cả hai thuật toán đều bằng \( O(N) \).
2. Locate smallest window to be sorted
Cho một mảng số nguyên, không theo một trong hai thứ tự tăng dần hoặc giảm dần. Viết hàm nhận mảng này làm input và xác định mảng con nhỏ nhất cần sắp xếp để mảng ban đầu trở thành một mảng sắp xếp. Do tính đối ngẫu nên mình chỉ xét trường hợp thứ tự sau khi thu được là tăng dần.
Example: với mảng \(input = [3, 7, 5, 6, 9] \), hàm của mình sẽ return \([1, 3]\) là vị trí index đầu và cuối của mảng con có độ dài nhỏ nhất trong mảng \( input \) cần sắp xếp.
Trong bài này, một kỹ thuật nữa mình muốn đề cập là hãy thử hình dung xem mảng của mình trước và sau khi sort có điểm gì giống và khác nhau.
Technique 2: Try to find out what the array elements would look like when sorted.
Với gợi ý này, quay lại bài toán mình có mảng \(input\) của mình sau khi sort là \([3, 5, 6, 7, 9]\), gọi \([left, right]\) là hai chỉ số đầu cuối của smallest window.
Để ý rằng hai phần tử đầu và cuối của mảng gốc và sau khi sorted là giống nhau, chỉ có các phần tử giữa là bị hoán đổi vị trí. Do đó, thuật toán của mình là đầu tiên thực hiện sort mảng theo thứ tự tăng dần \(inputSorted\), sau đó duyệt qua mảng \(input\) gốc để xem nếu \(input[i] \not\equiv inputSorted[i]\) và \(left \equiv null \) thì \(left = i \), ngược lại nếu \( input[i] \not\equiv inputSorted[i] \) thì \(right = i \).
function smallestWindow(input) {
if (input.length === 0) return [];
const inputSorted = [...input].sort((a, b) => a - b);
let left = null;
let right = null;
for (let i = 0; i < input.length; i++) {
if (input[i] !== inputSorted[i] && left === null) {
left = i;
} else if (input[i] !== inputSorted[i]) {
right = i;
}
}
return [left, right];
}
Thuật toán có time complexity bằng \( O(n\mathrm{log}n) \) do mình có thao tác sort lại mảng. Trong cài đặt JavaScript ở trên, mình thực hiện deep copy bằng spread operator để việc sort không ảnh hưởng vị trí các phần tử trên mảng gốc. Mọi người có thể tham khảo tại: developer.mozilla.org/en-US/docs/Web/JavaSc..
Follow-up: liệu mình có thể tìm ra \(left, right\) trong thời gian \(O(N) \)?
Câu trả lời là có thể, và kỹ thuật tiếp theo mình có thể áp dụng cho bài này là trong quá trình duyệt mảng, mình hoàn toàn có thể tính toán các phần tử có tính chất như: nhỏ nhất, lớn nhất hoặc đếm.
Technique 3: Looping through the elements and computing a running minimum, maximum, or count.
Trong cách sort mảng ở trên, thực sự mình không cần phải sort lại mảng để kiểm tra thông tin mà chỉ cần tính phần tử lớn nhất, \( currMax \) trong lúc duyệt và so sánh phần tử đang đứng \(input[i] \) với \(currMax\). Nếu \(input[i] < currMax\) thì \( input[i] \) chính phần tử trong mảng cần sort; tiếp tục duyệt sang bên phải, phần tử \(input[i]\) cuối cùng nhỏ hơn \(currMax\) chính là \(right\).
Một cách tương tự, mình duyệt từ cuối mảng lên và tìm phần tử \(input[i]\) cuối cùng vượt quá \(currMin\), đó chính là \(left\).
function smallestWindow2(input) {
if (input.length === 0) return [];
// Determine right bound
let currMax = Number.MIN_VALUE;
let right = null;
for (let i = 0; i < input.length; i++) {
if (input[i] < currMax) {
right = i;
} else {
currMax = input[i];
}
}
// Determine left bound
let currMin = Number.MAX_VALUE;
let left = null;
for (let i = input.length - 1; i >= 0; i--) {
if (input[i] > currMin) {
left = i;
} else {
currMin = input[i];
}
}
return [left, right];
}
Với thuật toán này, mình chỉ mất \(O(N)\) time complexity và \(O(1)\) space complexity.
3. Calculate maximum subarray sum
Cho một mảng gồm các số nguyên, viết hàm trả về tổng lớn nhất của các phần tử liên tiếp trong mảng con của mảng này.
Example: giả sử mảng được cho là \( input = [34, -50, 42, 14, -5, 86]\) thì giá trị trả về là \( 137 \) vì \(137 = 42 + 14 + -5 + 86 \), là giá trị lớn nhất của tổng các phần tử mảng con trong số các mảng con của \( input \).
Lời giải brute force cho bài này khá đơn giản, đầu tiên mình tạo một hàm tính tổng các phần tử trong mảng con từ \(i\) tới \(j\). Sau đó mình sẽ tạo tất cả các mảng con có thể của \( input \) bằng 2 vòng lặp tương ứng hai chỉ số đầu, cuối, tại mỗi mảng con, mình sẽ cập nhật giá trị \(currMax\).
function maxSum(input) {
if (input.length === 0) return 0;
function sumArr(i, j) {
let sum = 0;
for (let k = i; k <= j; k++) {
sum += input[k];
}
return sum;
}
let currMax = Number.MIN_VALUE;
for (let i = 0; i < input.length - 1; i++) {
for (let j = i + 1; j < input.length; j++) {
currMax = Math.max(currMax, sumArr(i, j));
}
}
return currMax;
}
Dễ thấy độ phức tạp của thuật toán brute force này là \(O(n^3) \). Và rất có thể đây không phải là lời giải mà chúng ta mong muốn, liệu có thuật toán nào chạy nhanh hơn không?
Technique 4: using Kadane's algorithm for calculating the sum of contiguous subarrays and finding the largest sum.
Cụ thể thuật toán này chỉ lặp qua mảng đúng một lần và tính 2 giá trị max là giá trị tổng lớn nhất khi duyệt tới vị trí \(i\), \(maxAtIndex\) (bằng cách so sánh xem có lấy phần tử thứ \(i\) cộng vào để được tổng lớn hơn hay không) và giá trị tổng lớn nhất của toàn mảng, \(maxGlobal\) (bằng cách so sánh và cập nhật nó với giá trị tổng lớn nhất khi duyệt tới vị trí thứ \(i\)).
function maxSum2(input) {
if (input.length === 0) return 0;
let maxAtIndex = 0;
let maxGlobal = 0;
for (let i = 0; i < input.length; i++) {
maxAtIndex = Math.max(input[i], maxAtIndex + input[i]);
maxGlobal = Math.max(maxGlobal, maxAtIndex);
}
return maxGlobal;
}
Độ phức tạp về thời gian của thuật toán Kadane là \(O(N)\) và về space là \(O(1)\).