Một số ghi chép về Lý thuyết đồ thị - phần 2
Table of contents
Sau khi tìm hiểu các khái niệm cơ bản và biểu diễn graph, bài này chúng ta cùng tìm hiểu về bài toán pathfinding và search xuất hiện rất nhiều trong lý thuyết đồ thị. Vì hầu hết các yêu cầu cần mình phải đi thăm một đỉnh nào đó hoặc một cạnh nào đó trong đồ thị, lớp bài toán này còn được gọi là graph traversal.
Trong bài này, class Graph mình sử dụng để biểu diễn đồ thị là graph có các adjacency lists được biểu diễn dưới dạng linked list được mình implement trong phần 1.
I. Breadth first search - BFS (Tìm kiếm chiều rộng):
Breadth first search là thuật toán tìm kiếm đơn giản nhất trong graph và có thể được sử dụng nhiều trong các thuật toán khác: thuật toán của Prim tìm cây khung nhỏ nhất, thuật toán Dijkstra tìm đường đi ngắn nhất cũng sử dụng ý tưởng giống với BFS. Thuật toán BFS thường tỏ ra hiệu quả khi mình cần tìm đường đi ngắn nhất (shortest path) trong một đồ thị không trọng số (unweighted graph).
Ý tưởng của thuật toán BFS là mình sẽ bắt đầu tại một node (thường gọi là source) của đồ thị sau đó "loang" ra các node kề (hoặc có cạnh nối) với node source, trước khi đi đến những node kề xa hơn.
Để biết được những node nào sẽ được thăm, BFS sử dụng một queue (hàng đợi) để lưu thông tin các node kề với node đang được thăm. Đây cũng là một khác biệt quan trọng của BFS với DFS, mình có thể viết DFS dưới dạng đệ quy (gọi lại hàn DFS(), giống hình ảnh của Stack - ngăn xếp) nhưng khi implement BFS thì cần nhớ thuật toán này sử dụng Queue. Đoạn mã giả dưới đây thể hiện ý tưởng của BFS:
function BFS(G, source) {
for each vertex u in G.V - {source} {
u.color = "WHITE"
u.d = Number.Infinite
u.p = null
}
source.color = "GRAY"
source.d = 0
source.p = null
Q = []
ENQUEUE(Q, source)
while (!Q.isEmpty()) {
u = DEQUEUE(Q)
for each v in G.Adj[u] {
if (v.color === "WHITE") {
v.color = "GRAY"
v.d = u.d + 1
v.p = u
ENQUEUE(Q, v)
}
}
u.color = "BLACK"
}
}
Về mặt giải thích cặn kẽ, mình thấy quyển Introduction to Algorithms khá tốt, các bạn có thể tham khảo.
Queue Q có thể được implement đơn giản bằng một mảng và hai thao tác enqueue, dequeue tương ứng với thao tác push và shift (để đảm bảo tính FIFO của queue) trong array.
function Queue() {
collection = [];
this.print = function () {
console.log(collection);
};
// this method push the first item into the queue (at the end of the array)
this.enqueue = function (element) {
collection.push(element);
};
// this method take the item off the queue
this.dequeue = function () {
return collection.shift(); // remove the first item of the array
};
this.front = function () {
return collection[0];
};
this.size = function () {
return collection.length;
};
this.isEmpty = function () {
return collection.length === 0;
};
}
Khi nói đến độ phức tạp của thuật toán BFS này, trong giải thuật trên, chúng ta có vòng lặp đầu tiên để khởi tạo những giá trị ban đầu cho các đỉnh trong \(G.V\) trừ đỉnh source (gốc), có \(O(V)\) time complexity. Các thao tác gán giá trị cho đỉnh source sau đó mất \(O(1)\). Việc enqueue và dequeue cũng mất thời gian \(O(1)\). Vòng lặp khi queue Q khác rỗng thực chất là mình đang đi duyệt tất cả các cạnh trong danh sách kề với đỉnh \(u\). Như vậy, khi vòng lặp kết thúc, tất cả các cạnh sẽ được duyệt nên mình có time complexity là \(O(E)\). Từ đó mình có thể kết luận độ phức tạp về mặt thời gian cho thuật toán này là \(O(V + E)\).
Bidirectional search
Bidirectional search được sử dụng để tìm đường đi ngắn nhất giữa 2 đỉnh source và destination. Thuật toán chạy hai hàm BFS, một bắt đầu từ đỉnh source và một bắt đầu từ đỉnh destination.
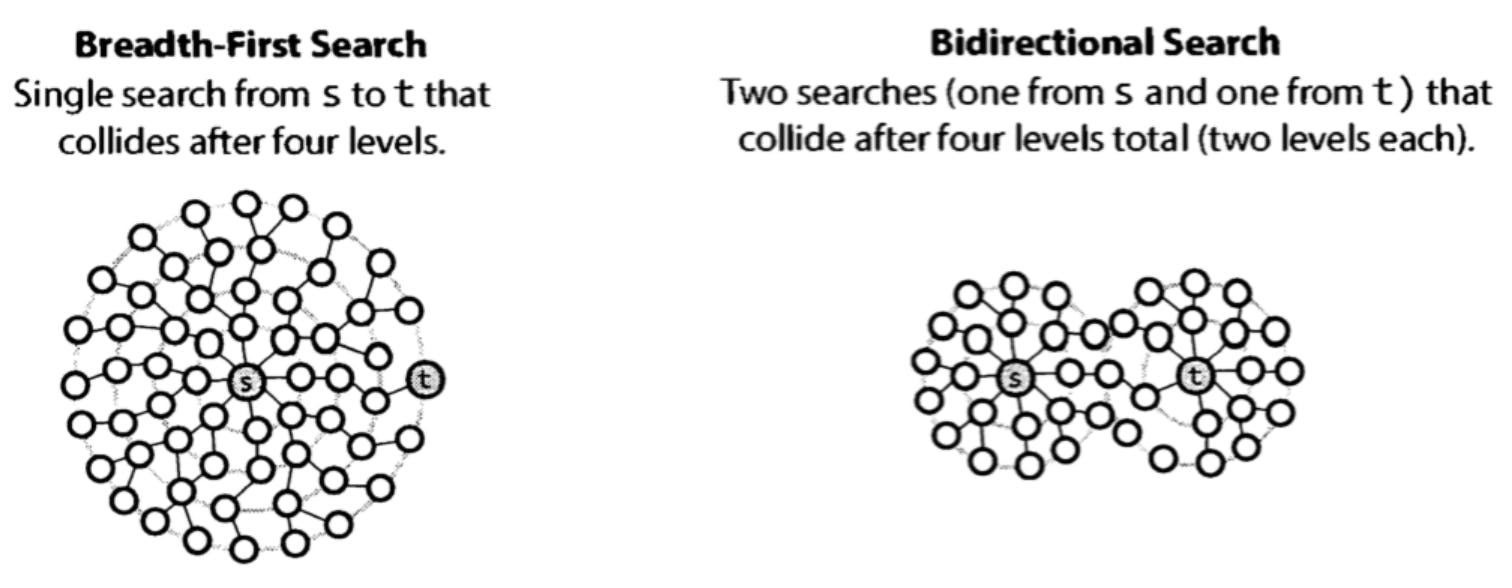
Trong thuật toán BFS nguyên thủy, mình search \(k\) nodes kề với node gốc, mỗi node kề lại có thể có thêm \(k'\) nodes kề với node kth. Nếu mình thực hiện \(d\) lần thì mình phải search qua \(O(k ^ {d})\) nodes. Ví dụ trong hình trên là \(d = 4\).
Bidirectional search sẽ giúp mình giảm xuống còn khoảng \(k ^ {d/2}\) nodes cho mỗi thuật toán chạy BFS từ đỉnh \(s\) và từ đỉnh \(t\).
II. Implement thuật toán BFS
Sau khi đã tìm hiểu ý tưởng của thuật toán BFS, mình sẽ implement thuật toán này với JavaScript. Yêu cầu của mình hiện tại là hàm bfs() sẽ nhận vào 2 tham số đầu vào tương ứng với 2 nodes \(s\) và \(e\) sau đó sẽ in ra đường đi ngắn nhất từ \(s\) tới \(e\) (nếu có) bằng thuật toán BFS.
Để thuận tiện, hàm bfs() của mình sẽ gọi lần lượt tới 2 hàm con là solve() và reconstructPath(). Như tên gọi, hàm solve(s) áp dụng thuật toán BFS tìm kiếm đường đi đến tất cả các đỉnh trong đồ thị bắt đầu từ đỉnh \(s\). Kết quả hàm solve(s) trả về là một mảng lưu thông tin \(prev\) với \(prev[i]\) cho biết node liền trước node \(i\) theo thuật toán BFS. Từ mảng \(prev\) này, hàm reconstructPath sẽ truy vết ngược lại và in ra đường đi ngắn nhất từ đỉnh \(s\) tới đỉnh \(e\), trường hợp không có sẽ trả về mảng rỗng.
function bfs(s, e) {
// Do a BFS starting at node s
let prev = solve(s);
// Return reconstructed path from s to e
return reconstructPath(s, e, prev);
}
function solve(s) {
let q = [];
q.push(s); // enqueue method: push node into the array
let visited = new Array(graph.vertices).fill(false);
visited[s] = true;
let prev = new Array(graph.vertices).fill(null);
while (q.length) {
let node = q.shift(); // dequeue method: shift first node (s) from the array
let neighbors = graph.edges[node]; // get all neighbors (nodes) in adjacency list of s
let curr = neighbors.head;
while (curr) {
if (!visited[curr.data]) {
if (!q.includes(curr.data)) {
q.push(curr.data);
}
visited[curr.data] = true;
prev[curr.data] = node;
}
curr = curr.next;
}
}
return prev;
}
function reconstructPath(s, e, prev) {
let path = [];
for (let i = e; i !== null; i = prev[i]) {
path.push(i);
}
path.reverse();
if (path[0] === s) {
return path;
}
return [];
}
console.log(bfs(0, 3)); // Returns [0, 1, 3]
Việc chứng minh đường đi (nếu có) từ \(s\) đến \(e\), trong trường hợp test của mình là từ \(0\) đến \(3\) theo BFS cũng chính là đường đi ngắn nhất từ \(s\) đến \(e\) ( từ \(0\) đến \(3\)) (theo định nghĩa đi qua ít cạnh nhất), các bạn có thể xem trong sách Introduction to Algorithms, CLRS (implement bằng mã giả) hoặc tài liệu của thầy Lê Minh Hoàng (implement bằng Pascal).
Thử một đồ thị có nhiều đỉnh và cạnh hơn để xem thuật toán của mình chạy như thế nào:
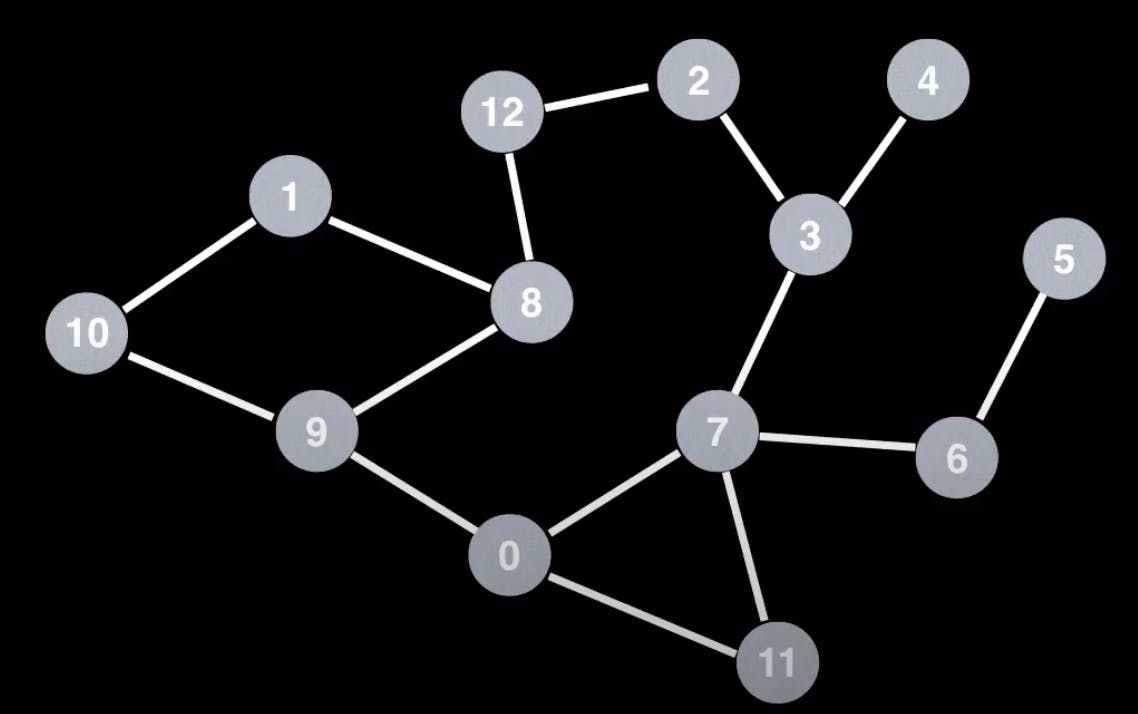
const graph = new Graph(13);
graph.addEdge(1, 10);
graph.addEdge(1, 8);
graph.addEdge(0, 9);
graph.addEdge(0, 7);
graph.addEdge(0, 11);
graph.addEdge(9, 8);
graph.addEdge(8, 12);
graph.addEdge(2, 12);
graph.addEdge(3, 4);
graph.addEdge(3, 2);
graph.addEdge(3, 7);
graph.addEdge(7, 11);
graph.addEdge(6, 7);
graph.addEdge(5, 6);
graph.addEdge(10, 9);
console.log("BFS shortest path from 5 -> 12: ", bfs(5, 12)); // returns [5, 6, 7, 3, 2, 12]
console.log("BFS shortest path from 0 -> 11", bfs(0, 11)); // returns [0, 11]
console.log("BFS shortest path from 11 -> 3", bfs(11, 3)); // returns [11, 7, 3]
console.log("BFS shortest path from 0 -> 12", bfs(0, 12)); // returns [0, 9, 8, 12]
Ngoài ra, cách cài đặt trên cho hàm bfs() cho phép mình trả lời được câu hỏi: Cho một đồ thị (có thể vô hướng hoặc không), xác định liệu có đường đi nối giữa hai đỉnh cho trước hay không. Mình sẽ đi sâu vào ứng dụng của BFS và DFS trong các bài tiếp theo.
III. Depth First Search - DFS (Tìm kiếm chiều sâu)
Tương tự như thuật toán BFS, mình cũng sẽ tìm hiểu template của thuật toán DFS trước bằng mã giả sau đó implement chi tiết bằng JavaScript.
Thuật toán DFS ưu tiên duyệt theo chiều "sâu". Bắt đầu từ node \( source \), DFS sẽ duyệt các node thuộc cùng một nhánh đến khi không thể đi xa hơn được nữa, mình mới chuyển sang duyệt nhánh tiếp theo (đệ quy backtrack). Thuật toán cứ tiếp tục đến khi tất cả các cạnh của đồ thị được duyệt quạ
Như vậy, có thể thấy về mặt time complexity, DFS cũng giống như BFS là \( O(V + E) \).
Trong các bài toán tìm đường đi ngắn nhất hoặc duyệt để kiểm tra có hay không đường đi giữa các đỉnh thì thuật toán BFS tỏ ra hiệu quả hơn dù phần cài đặt cần nhiều kỹ thuật một chút . DFS sẽ không có hiệu quả khi implement thuần túy, tuy nhiên ý tưởng của DFS sẽ rất hiệu quả trong các thuật toán quan trọng của đồ thị về tìm thành phần liên thông, liên thông mạnh, xác định khớp đồ thị, ...
Ý tưởng của DFS được thể hiện qua đoạn mã giả bên dưới.
function DFS(G) {
for each vertex u in G.V {
u.color = "WHITE"
u.p = null
}
time = 0
for each vertex u in G.V {
if u.color === "WHITE"
VISIT(G, u)
}
}
function VISIT(G, u) {
time = time + 1
u.d = time
u.color = "GRAY"
for each v in G.adj[u] {
if v.color === "WHITE"
v.p = u
VISIT(G, v)
u.color = "BLACK"
time = time + 1
u.f = time
}
}
Đoạn mã này, tương tự như đoạn mã của BFS, mình lấy trong cuốn Introduction to Algorithms, CLRS. Sách giải thích rất kĩ từng dòng và việc tô màu các đỉnh dựa trên 3 trạng thái trong quá trình duyệt cũng giúp mình dễ hình dung hơn.
IV. Implement thuật toán DFS
Bây giờ mình sẽ implement thuật toán DFS bằng ngôn ngữ JavaScript. Để thuận tiện mình sẽ không đánh dấu hay tô màu các đỉnh dựa vào trạng thái của chúng trong quá trình duyệt như mã giả ở trên, thay vào đó mình dùng một mảng visited[] (giống như phần implement BFS) để đánh dấu xem nếu visited[i] = true thì đỉnh \( i \) đã được duyệt, ngược lại ban đầu tất cả các đỉnh chưa được duyệt qua thì visited[i] = false.
Chương trình dfs() nhận tham số đầu vào là \( s \), đỉnh bắt đầu duyệt và có chương trình con visit() để thực hiện thăm tất cả các đỉnh theo ý tưởng DFS nếu đỉnh đó trong mảng đánh dấu visited[] là chưa được thăm.
Thủ tục đệ quy visit() sẽ bắt đầu bằng lời gọi visit(s).
function dfs(s) {
let visited = new Array(graph.vertices).fill(false);
let visit = (at) => {
if (visited[at]) return;
visited[at] = true;
let neighbors = graph.edges[at];
let curr = neighbors.head;
while (curr) {
visit(curr.data);
curr = curr.next;
}
};
return visit(s);
}
Để kiểm tra xem hàm dfs() của mình duyệt đúng hay không, mình sẽ thử với test case đồ thị có 13 đỉnh, 15 cạnh giống như hàm bfs() ở trên. Mình sẽ thêm vào trước bước visited[at] = true một dòng console.log("visit node: ", at); để log ra màn hình node mà hàm dfs() đang duyệt.
Khi đó kết quả ở màn hình console mình thu được như sau:
visit node: 0
visit node: 9
visit node: 8
visit node: 1
visit node: 10
visit node: 12
visit node: 2
visit node: 3
visit node: 4
visit node: 7
visit node: 11
visit node: 6
visit node: 5
Sau khi đối chiếu với hình minh họa của đồ thị này trong phần BFS ở trên, mình thấy kết quả duyệt theo DFS là đúng.
Như đã nói, thuật toán DFS sẽ rất hữu dụng trong việc xác định các connected components của đồ thị nên mình sẽ thử áp dụng ý tưởng DFS trên cho bài toán này. Các ứng dụng khác của DFS sẽ được nói đến ở các bài sau.
V. Connected Component
Connected components có thể được định nghĩa là những vùng thuộc đồ thị, bao gồm các đỉnh sao cho 2 đỉnh \( x \), \( y \) bất kỳ trong 1 component mình luôn có:
- luôn tồn tại đường đi từ \(x \) đến \(y\)
- đồng thời gọi \(xA\) là đỉnh thuộc component \(A\) và \(xB\) là đỉnh thuộc component \(B\) khi đó cạnh \( (xA, yB) \) không thuộc \( E \) và không tồn tại đường đi từ \(xA\) đến \(xB\)
Các components này chia graph ban đầu thành những vùng khác nhau, mình có thể phân biệt các vùng này bằng cách đánh dấu các đỉnh thuộc cùng một component thành 1 màu. Việc tô màu các đỉnh tương đương với việc mình label các đỉnh trong component đó bằng cùng một giá trị nào đó, có thể là \( (0, 1, 2, ...) \) giống như hình minh họa dưới đây:
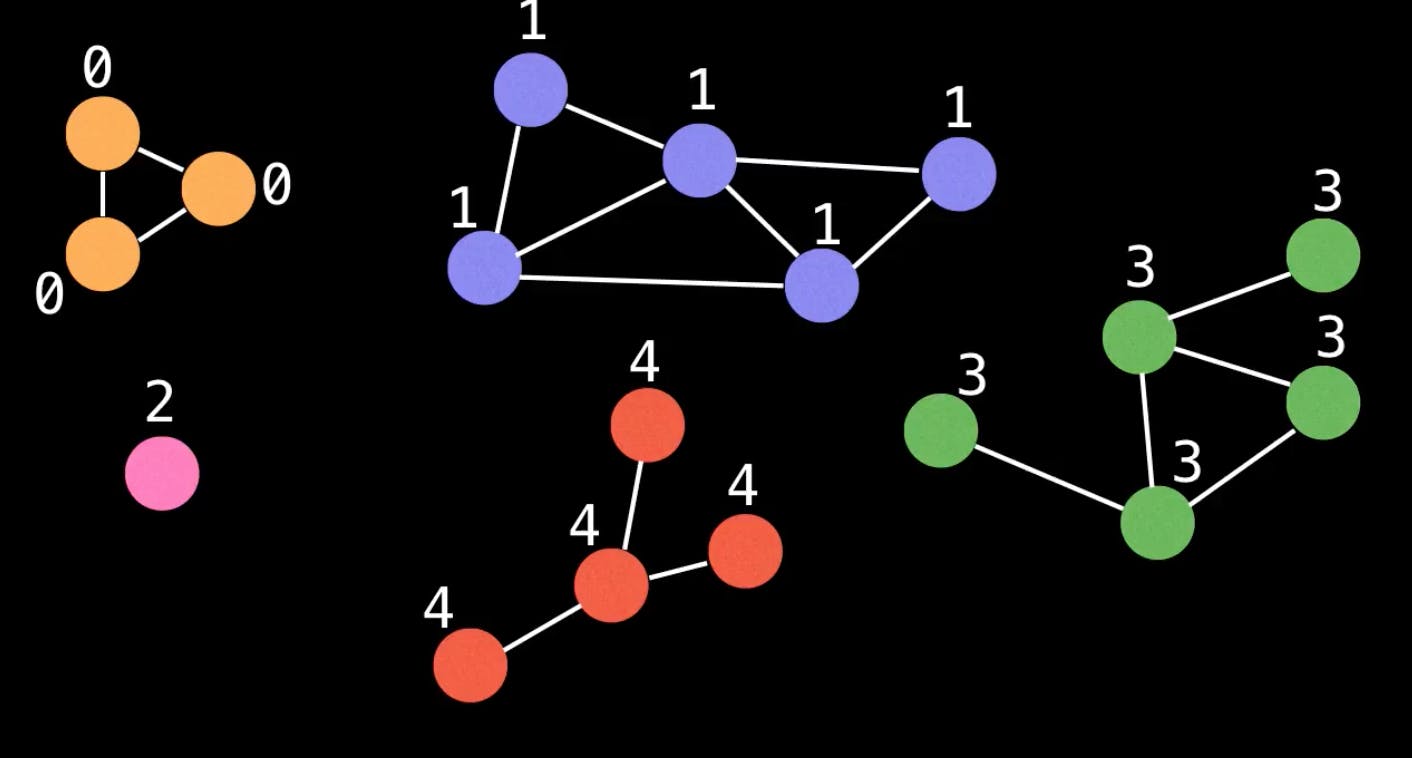
Giả sử ban đầu các đỉnh chưa được tô màu, mình sẽ tạo một đồ thị như hình trên và đánh số các đỉnh theo thứ tự từ \( 0 ... 17 \).
let newGraph = new Graph(18);
newGraph.addEdge(0, 4);
newGraph.addEdge(0, 8);
newGraph.addEdge(0, 13);
newGraph.addEdge(0, 14);
newGraph.addEdge(14, 8);
newGraph.addEdge(13, 14);
newGraph.addEdge(4, 8);
newGraph.addEdge(1, 5);
newGraph.addEdge(17, 5);
newGraph.addEdge(5, 16);
newGraph.addEdge(6, 11);
newGraph.addEdge(11, 7);
newGraph.addEdge(7, 6);
newGraph.addEdge(3, 9);
newGraph.addEdge(9, 2);
newGraph.addEdge(2, 15);
newGraph.addEdge(9, 15);
newGraph.addEdge(10, 15);
Thuật toán ở đây là mình cũng sẽ cần một mảng đánh dấu xem node thứ \( ith \) đã được duyệt qua hay chưa là visited[]. Bắt đầu từ một node chưa được duyệt, thuật toán DFS sẽ duyệt qua tất cả các node đồng thời label các node này bằng một id giống nhau, ví dụ ban đầu mình có thể để id = 0 hoặc id = 1.
Hàm findComponents() trả về 2 giá trị count là số connected components có trong graph và mảng components[] cho biết thông tin node thứ \( i_{th} \) thuộc component thứ \( components[i] \).
function findComponents() {
let count = 0;
let components = [];
let visited = new Array(newGraph.vertices).fill(false);
for (let i = 0; i < newGraph.vertices; i++) {
if (!visited[i]) {
count++;
visit(i);
}
}
function visit(at) {
visited[at] = true;
components[at] = count;
let neighbors = newGraph.edges[at];
let curr = neighbors.head;
while (curr) {
if (!visited[curr.data]) {
visit(curr.data);
}
curr = curr.next;
}
}
return {
count: count,
components: components,
};
}
console.log("Find components: ", findComponents());
Kết quả ở màn hình console của mình:
Find components: {
count: 5,
components: [
1, 2, 3, 3, 1, 2, 4,
4, 1, 3, 3, 4, 5, 1,
1, 3, 2, 2
]
}
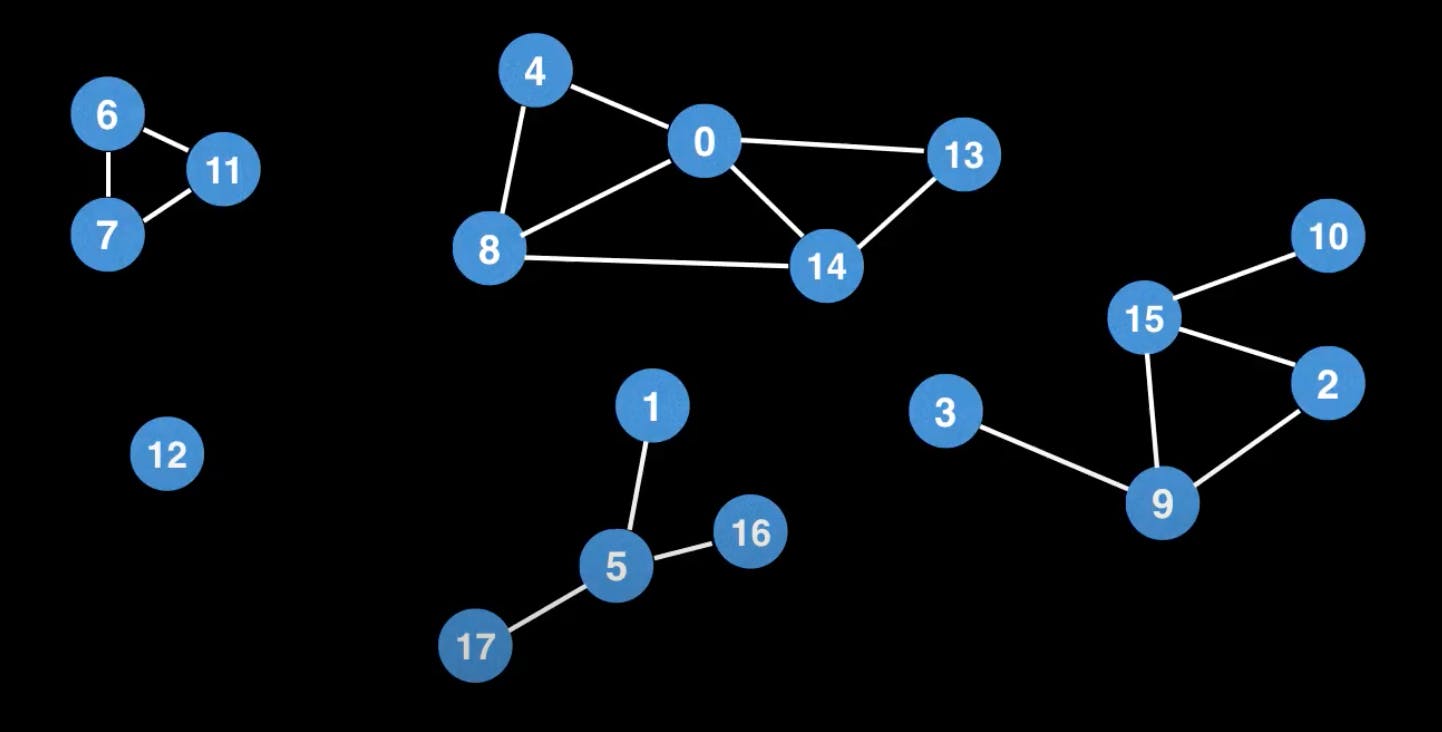
Từ mảng components[] mà hàm findComponents() trả về mình thấy các node \( (0, 4, 8, 13, 14) \) thuộc cùng một component được label là \( 1 \) ... Đúng với hình vẽ minh họa newGraph ở trên.
Ngoài ra, mảng components[] được trả về từ hàm findComponents() cho phép mình liệt kê thông tin của tất cả các connected components trong graph.
Bằng cách sử dụng Map, mình sẽ lưu thông tin của các đỉnh thuộc cùng một components và in ra thông tin của map này. Giả sử mình đã có mảng components[], chương trình in ra các connected components của mình như sau:
let map = new Map();
for (let i = 0; i < components.length; i++) {
if (map.has(`Connected component ${components[i]}`)) {
map.get(`Connected component ${components[i]}`).push(i);
} else {
map.set(`Connected component ${components[i]}`, [i]);
}
}
console.log("Connected Components: ", map);
Thử chạy và kiểm tra kết quả trên màn hình console:
Connected Components: Map {
'Connected component 1' => [ 0, 4, 8, 13, 14 ],
'Connected component 2' => [ 1, 5, 16, 17 ],
'Connected component 3' => [ 2, 3, 9, 10, 15 ],
'Connected component 4' => [ 6, 7, 11 ],
'Connected component 5' => [ 12 ]
}
Trong chương trình in ra các connected components, mình tạo ra một map = new Map() để lưu trữ và các thao tác get và set mất thời gian \( O(1) \). Bên cạnh đó, mình dùng một vòng for để duyệt qua tất cả phần tử của components[] nên sẽ mất thời gian là \( O(N) \) với \(N\) là độ dài mảng components[] hay chính là số đỉnh graph.vertices của đồ thị, \( O(V) \). Do đó, độ phức tạp time complexity của chương trình này là \( O(V) \).
Xác định các connected components bằng BFS
Trong thuật toán tìm thành phần liên thông (Connected Components) ở trên, mình đã sử dụng ý tưởng duyệt DFS. Nếu quan sát kỹ đồ thị ở ví dụ này, mình vẫn có thể xác định các thành phần liên thông bằng thuật toán duyệt BFS.
Cụ thể, thay vì duyệt từ đỉnh 0 (ví dụ) rồi đi đến một đỉnh nào đó có cạnh nối với 0, ... thì mình sẽ duyệt theo BFS "loang" ra tất cả các đỉnh kề với đỉnh 0, những đỉnh này chắc chắn sẽ thuộc chung một connected components và sẽ được label chung một chỉ số.
Chương trình dưới đây implement bằng JavaScript cho thuật toán tìm thành phần liên thông theo BFS.
function findConnectedComponentBFS() {
let components = [];
let visited = new Array(newGraph.vertices).fill(false);
let count = 0;
for (let i = 0; i < visited.length; i++) {
if (!visited[i]) {
count++;
bfs(i);
}
}
function bfs(at) {
let q = [];
q.push(at);
visited[at] = true;
components[at] = count;
while (q.length) {
let node = q.shift();
let neighbors = newGraph.edges[node];
let curr = neighbors.head;
while (curr) {
if (!visited[curr.data]) {
if (!q.includes(curr.data)) {
q.push(curr.data);
}
visited[curr.data] = true;
components[curr.data] = count;
}
curr = curr.next;
}
}
}
return components;
}
console.log("Connected Components BFS: ", findConnectedComponentsBFS());
Thử chạy chương trình và so sánh components[] trả về với kết quả của hàm findComponents() dùng DFS:
Connected Components BFS: [
1, 2, 3, 3, 1, 2, 4,
4, 1, 3, 3, 4, 5, 1,
1, 3, 2, 2
]
Từ kết quả trả về của hàm findConnectedComponentsBFS(), mình hoàn toàn có thể xây dựng chương trình in ra thông tin của các components[] giống như ví dụ DFS.
Cài đặt thuật toán DFS bằng cách khử đệ quy
Chương trình DFS ở trên mình dùng đệ quy để gọi lại hàm visit(), có một cách khác để cài đặt là sử dụng một stack để lưu lại các đỉnh cần thăm. Bởi vì hình ảnh hàm visit(at) được gọi và xóa đi sau khi gọi xong giống với hình ảnh push và pop một đỉnh kề ra khỏi stack sau khi duyệt xong.