Chris Dinh - Software Engineer @ NAB

Một số ghi chép về Lý thuyết đồ thị - phần 1

Chau Dinh (Chris)'s photo
Chau Dinh (Chris)

Table of contents

Dưới đây là ghi chép của mình về một số kiến thức cơ bản trong quá trình học ‌Data Structures and ‌Algorithms. Đây chỉ là cách mình implements và một số ghi chép về tính hiệu quả, tradeoffs nên nó không thể xem như là tài liệu để học. Các bạn có thể tham khảo 3 cuốn sách là

  • Introduction to Algorithms - CLRS

  • The Algorithm Design Manual - Steven Skiena

  • Cracking The Coding Interviews

I. Graph

Một số khái niệm trong đồ thị:

  • Undirected graph: \(G = (V, E)\) gọi là undirected nếu như \((x, y)\) thuộc E thì ta cũng có \((y, x)\) thuộc \(E\). Ngược lại, ta gọi là directed.

  • Weighted vs. Unweighted: mỗi cạnh của G có thể được gán với một giá trị nào đó, hay còn gọi là trọng số (weight).

  • Simple vs. Non-simple: một cạnh \((x, y)\) xuất hiện nhiều hơn 1 lần trong graph được gọi là ‌multiedge. Các graph không có ‌multiedge được gọi là simple (đơn).

  • Sparse vs. Dense: đồ thị có số cạnh gần như đầy đủ giữa tất cả các đỉnh được gọi là dense, ngược lại, đồ thị có ít cạnh nối giữa các đỉnh được gọi là sparse. Đây là hai khái niệm không tuyệt đối, thường phụ thuộc vào ngữ cảnh của từng bài toán.

  • Cyclic vs. Acyclic: đồ thị không có vòng (cycle) được gọi là acyclic. Trees có thể xem là một acyclic. Ngoài ra, tree còn có một tính chất khá thú vị là nếu ta cắt một lá bất kỳ của tree thì ta sẽ thu được 2 tree mới (tính recursive). Directed acyclic graphs thường được ứng dụng trong các bài toán lập lịch (scheduling). Trong đó, cạnh \((x, y)\) biểu diễn hành động \(x\) cần xảy ra trước, hoặc thực hiện trước hành động \(y\).

  • Ngoài ra, còn một số khái niệm về bán bậc vào, bán bậc ra, implicit/explicit. Dưới đây là minh họa một số khái niệm mình đã nêu ở trên.

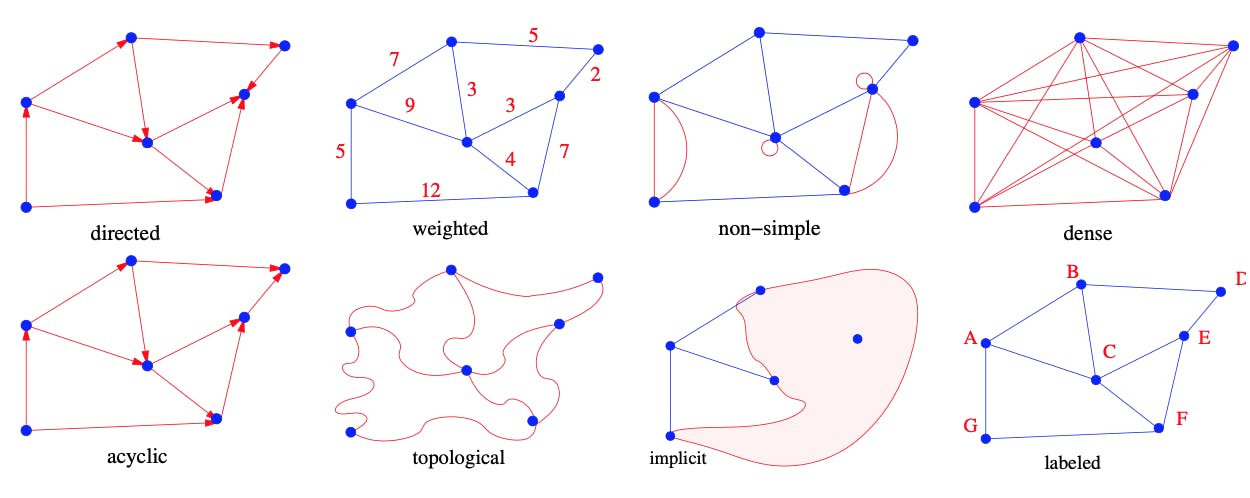
graph-notes-1-first.png

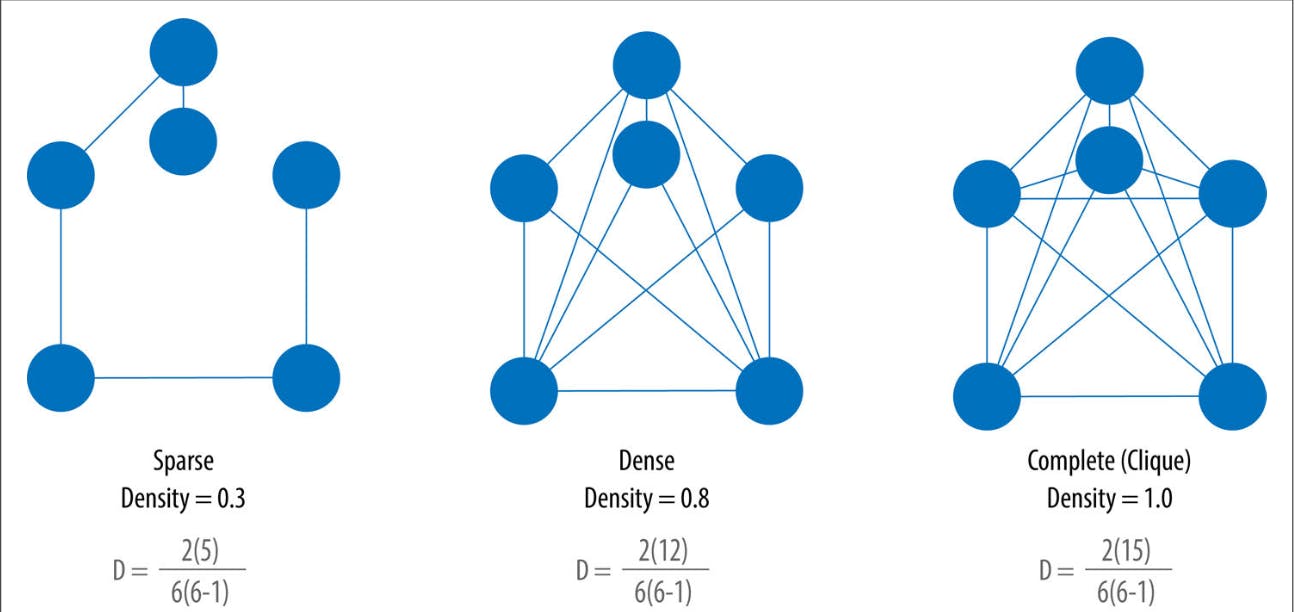
Có thể thấy việc định nghĩa sparse và dense của graph ở trên khá mơ hồ, có một cách minh họa cho vấn đề này là ta sẽ xem xét nếu như một graph có số cạnh nối giữa các đỉnh là tối đa thì “độ dày” của graph = 1, ngược lại, độ dày này sẽ dao động giữa khoảng \([0, 1]\). Từ đây ta có thể rút ra được công thức tính số cạnh tối đa có thể nối trong một graph với N đỉnh cho trước là: MaxD=N(N−1)2

Và độ dày thực tế của một graph được tính bằng công thức, với R là số cạnh thực tế thuộc E: D=2RN(N−1)

Từ công thức trên, ta suy ra nếu \(R = MaxD\) thì \(D = 1\), ngược lại \(D\) sẽ nhận các giá trị trong khoảng \([0, 1]\). Do đó, ta có thể xem xét những graph nào có \(D\) càng tiến gần về 1 thì là dense, ngược lại, có \(D\) càng tiến gần về 0 thì là sparse.

graph-notes-1-forth.png

II. Biểu diễn graph

Giống như các cấu trúc trừu tượng khác, việc ta chọn lựa cấu trúc để biểu diễn Graph sẽ có ảnh hưởng đến performance. Thường có hai cách để biểu diễn là dùng ‌Adjacency matrix và ‌Adjacency list

  • Adjacency matrix: biểu diễn graph \(G = (V, E)\) bằng một ma trận \(n \times n\), trong đó \(M[i, j] = 1\) nếu \((i, j)\) là một cạnh thuộc \(E\) và \(M[i, j] = 0\) nếu \((i, j)\) không thuộc \(E\).

  • Adjacency list: chúng ta có thể sử dụng linked list để biểu diễn những đỉnh kề với mỗi đỉnh thuộc \(V\) của đồ thị. Cụ thể, có 2 cách để implement danh sách kề phổ biến là: forward star - với mỗi đỉnh \(u\) ta lưu trữ một danh sách \(adj[u]\) chứa các đỉnh nối từ \(u\) và reverse start - khi đó danh sách \(adj[u]\) chứa các đỉnh nối tới \(u\).

Về ưu điểm thì biểu diễn đồ thị bằng ma trận kề (adjacency matrix):

  • Đơn giản, trực quan, dễ cài đặt

  • Dễ dàng kiểm tra một cạnh \((u, v)\) bất kỳ có thuộc \(E\) hay không bằng cách so sánh a[uv] === 0

Tuy nhiên nhược điểm của cách cài đặt này là luôn đòi hỏi cần có \(n^{2}\) ô nhớ dù số cạnh của đồ thị có thể là rất ít (sparse graph). Ngoài ra, khi yêu cầu cần liệt kê tất cả các đỉnh \(u\) kề với một đỉnh \(v\) cho trước thì ta phải xét tất cả các đỉnh \(u\) và kiểm tra điều kiện a[vu] !== 0. Adjacency list (danh sách kề) sẽ giúp ta khắc phục được những nhược điểm này.

Thực tế, người ta thường áp dụng cách biểu diễn bằng danh sách kề hơn và mình cũng sẽ chỉ đi vào implement cách này. Ngoài ra có một bảng so sách để mọi người dễ tham khảo giữa hai cách dùng ma trận kề và danh sách kề được đề cập trong sách của Skiena:

graph-notes-1-second.png

Tương tự như cách làm với linked list, mình sẽ đi xác định thành phần node, ở đây là mỗi cạnh kề tương ứng với mỗi đỉnh:

class EdgeNode {
  constructor(y, weight = null, next = null) {
    this.y = y; // adjacency info
    this.weight = weight; // edge weight, if any
    this.next = next; // next edge in list
  }
}

Việc biểu diễn graph bây giờ chỉ cần ta sử dụng một mảng edges mô tả phần tử thứ \(i\) (edges[i]) là danh sách cạnh kề với đỉnh \(i\). Ngoài ra, có thể bài toán yêu cầu thêm bậc ra degree tại một đỉnh nên ta sẽ thêm vào graph mảng degree với phần tử degree[i] mô tả bậc ra tại đỉnh \(i\).

class Graph {
  constructor(
    edges = [],
    degree = [],
    nvertices = 0,
    nedges = 0,
    directed = false
  ) {
    this.edges = edges; // adjacency info
    this.degree = degree; // outdegree of each vertex
    this.nvertices = nvertices; // number of vertices
    this.nedges = nedges; // number of edges
    this.directed = directed; // is the graph directed?
  }
}

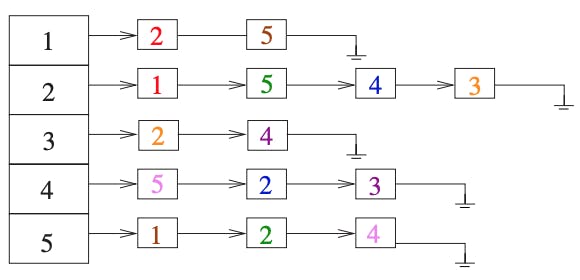
graph-notes-1-third.png

Lưu ý rằng, khi graph là một undirected thì cạnh \((x, y)\) sẽ xuất hiện 2 lần trong danh sách kề, một lần với \(y\) thuộc danh sách kề của \(x\) và một lần \(x\) thuộc danh sách kề của \(y\). Ngoài ra, khi đồ thị cho là một đồ thị vô hướng, không có trọng số thì ta có thể giản lược danh sách kề thành mảng các đỉnh kề với đỉnh \(i\). Ví dụ như: {1: [2, 4]}, chúng ta sẽ xem xét implement trường hợp đơn giản này trước:

class Graph {
  constructor() {
    this.adjacencyList = {};
  }

  addVertex(vertex) {
    if (!this.adjacencyList[vertex]) {
      this.adjacencyList[vertex] = [];
    }
  }

  addEdge(source, destination) {
    if (!this.adjacencyList[source]) {
      this.addVertex(source);
    }
    if (!this.adjacencyList[destination]) {
      this.addVertex(destination);
    }
    this.adjacencyList[source].push(destination);
    this.adjacencyList[destination].push(source);
  }

  removeEdge(source, destination) {
    this.adjacencyList[source] = this.adjacencyList[source].filter(
      (vertex) => vertex !== destination
    );
    this.adjacencyList[destination] = this.adjacencyList[destination].filter(
      (vertex) => vertex !== source
    );
  }

  removeVertex(vertex) {
    while (this.adjacencyList[vertex]) {
      const adjacencyVertex = this.adjacencyList[vertex].pop();
      this.removeEdge(vertex, adjacencyVertex);
    }
    delete this.adjacencyList[vertex];
  }

  printGraph() {
    return this.adjacencyList;
  }
}

Việc thêm đỉnh mới vào trong graph đơn giản là ta kiểm tra xem đỉnh đó đã có trong adjacencyList chưa, nếu chưa thì ta tạo mới và gán cho nó một mảng rỗng danh sách các đỉnh kề với nó.

Hàm addEdge thêm một cạnh mới vào đồ thị, do đây ta quy ước là undirected graph nên ta phải thêm vào 2 chỗ: một là trong danh sách kề của source và một trong danh sách kề của destination. Xóa một cạnh đơn giản là xóa đỉnh kề trong 2 danh sách kề của source và destination.

Hàm xóa một đỉnh phức tạp hơn một chút. Trước khi xóa một đỉnh, ta sẽ duyệt qua toàn bộ các đỉnh có nối tới đỉnh đó và xóa các cạnh này đi.

Trường hợp tổng quát hơn, đồ thị có thể có trọng số thì ta sẽ implement danh sách kề bằng linked list như đã nói ở đầu.

Trước tiên, mình cần implement một linked list (singly linked list) và thao tác để chèn các node kề vào. Do việc chèn các đỉnh kề với một đỉnh trong adjacency list không quan trọng thứ tự trước sau, nên mình có thể chèn lên đầu linked list hoặc cuối. Mình sẽ implement cả hai thao tác để tham khảo:

class Node {
  constructor(data, next = null) {
    this.data = data;
    this.next = next;
  }
}

class LinkedList {
  constructor() {
    this.head = null;
    this.size = 0;
  }

  // Insert first node
  insertFirst(data) {
    this.head = new Node(data, this.head);
    this.size++;
  }

  // Insert last node
  insertLast(data) {
    let node = new Node(data);
    let current;

    // If empty, make this node as the head
    if (!this.head) {
      this.head = node;
    } else {
      current = this.head;
      while (current.next) {
        current = current.next;
      }

      current.next = node;
    }

    this.size++;
  }
// ... other methods
}

Mình sẽ dùng thao tác insertFirst() để thêm các node vào adjacency list sau đây:

const LinkedList = require("../Linked Lists/index");

class Graph {
  constructor(vertices, edges = []) {
    this.vertices = vertices;
    this.edges = edges;
    for (let i = 0; i < vertices; i++) {
      let temp = new LinkedList();
      this.edges.push(temp);
    }
  }

  addEdge(source, destination) {
    this.edges[source].insertFirst(destination);
    this.edges[destination].insertFirst(source);
  }
}

const graph = new Graph(5);
console.log(graph);
graph.addEdge(0, 1);
graph.addEdge(0, 4);
graph.addEdge(1, 4);
graph.addEdge(1, 3);
graph.addEdge(1, 2);
graph.addEdge(2, 3);
graph.addEdge(3, 4);
console.log(graph);

Thử minh họa hình biểu diễn graph bằng Adjacency List phía trên, ta thu được kết quả đúng như mong muốn:

Graph {
  vertices: 5,
  edges: [
    LinkedList { head: [Node], size: 2 },
    LinkedList { head: [Node], size: 4 },
    LinkedList { head: [Node], size: 2 },
    LinkedList { head: [Node], size: 3 },
    LinkedList { head: [Node], size: 3 }
  ]
}

Ta có thể insert đỉnh kề mới vào đầu hoặc cuối danh sách linked list đều được. Như vậy, có thể thấy việc implement adjacency list bằng linked list tốn khá nhiều thời gian và phức tạp hơn so với mảng thông thường. Nên trừ khi trường hợp bài toán bắt buộc, mình sẽ dùng cách adjacency list để biểu diễn đồ thị và implement các cạnh kề bằng mảng.

III. Một số dạng thuật toán trong Graph

Graph có khá nhiều ứng dụng, việc nghiên cứu về graph có thể xem như là một công việc phân tích, đưa ra các thuật toán cho các vấn đề cần giải quyết. Có 3 kiểu phân tích bao hàm khá nhiều thuật toán quan trọng trong graph là pathfinding and search, centrality computation và community detection.

IV. Pathfinding

Bài toán tìm đường đi ngắn nhất, đường đi có chi phí nhỏ nhất trong đồ thị có trọng số là một ví dụ kinh điển trong lớp các bài toán này. Trong thực tế việc tìm ra shortest path hoặc avarage shortest path giúp ta xác định được avarage distance giữa các node, ở đây có thể là nhà ga, bến xe... Thỉnh thoảng ta cũng cần tìm longest path.

Một số thuật toán nổi tiếng trong dạng toán này là:

  • Thuật toán tìm đường đi ngắn nhất, shortest path, giữa hai đỉnh (nodes) cho trước (A* and Yen's)

  • Thuật toán tìm đường đi ngắn nhất giữa mọi cặp đỉnh, hoặc tìm đường đi ngắn nhất từ một đỉnh cho trước đến các đỉnh còn lại

  • Minimum spaning tree (cây khung nhỏ nhất)

  • Random walk

V. Centrality

Đúng như tên gọi, bài toán yêu cầu xác định node nào là "trung tâm" trong một graph. Tùy vào ngữ cảnh cụ thể mà ta định nghĩa từ "trung tâm" này khác nhau.

VI. Community detection

Trong một graph có thể tồn tại nhiều graph con (subgraph), điều này xuất hiện khá thường xuyên trong các bài toán thực tế liên quan đến mạng xã hội. Yêu cầu của dạng bài này là xác định những subgraph này. Trong bài tiếp theo chúng ta sẽ nói và implement một số thuật toán mình đã liệt kê trong phần pathfinding and search.

algorithmsdata structuresJavaScript